poltcourt.blogg.se - 0 1 knapsack

The weights and the values associated with items are shown in the diagram. Let's suppose we have a knapsack with a maximum weight limit of 50 units and three items namely item1, item2, and item3. However, this greedy approach will fail for the input shown in the diagram above. Then use the same algorithm to fill the remaining capacity of the knapsack. One may try to solve the problem using a greedy approach where we greedily pick the item with the maximum value such that its weight is less than or equal to W (maximum limit of knapsack). Greedily selecting the item with the maximum value to fill the knapsack.Īs we want to find the maximum sum of the values of the items that can be filled in the knapsack. Let us consider two examples where the greedy solution fails. We can't use a greedy algorithm to solve the 0-1 knapsack problem as a greedy approach to solve the problem may not ensure the optimal solution. In this section, we will try to build the logic for the 0-1 knapsack problem.

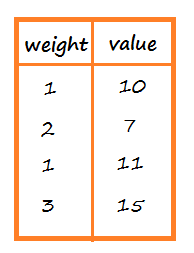
You can not partially fill an item in the knapsack. value and weight will store the value and weight associated with ith item. You have to fill the knapsack in such a way so that the total weight of the filled items is less than or equal to W and the sum of the values of the filled items is maximum. Given a Knapsack with maximum weight limit as W and two arrays value and weight. There is no option of partially keeping an item in the knapsack, unlike the Fractional Knapsack problem. In the 0-1 Knapsack Problem we can either decide to keep an item in the knapsack or not keep an item in the knapsack.

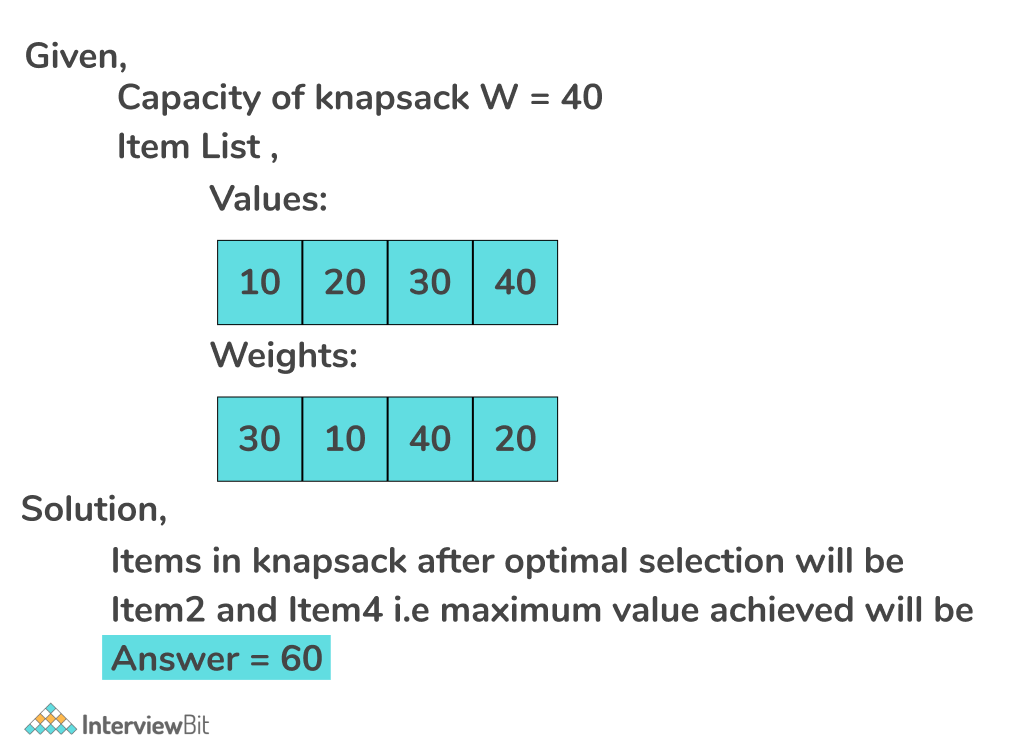
We can not fill all the items in the knapsack as the total weight of all the items will exceed the maximum weight limit of the knapsack. If we try out all the valid combinations in which the total weight of the filled items is less than or equal to 30, we will see that we can get the optimal answer by selecting item2 and item3 in the knapsack which gives us a total value of 120. Now we have to fill the knapsack in such a way so that the sum of the values of items filled in the knapsack is maximum. The values and weights associated with each item are shown in the diagram. We have three items namely item1, item2, and item3. The diagram above shows a Knapsack that can hold up to a maximum weight of 30 units. Select item 2 and Item 3 which will give us total value of 140 + 60 = 200 which is the maximum value we can get among all valid combinations. Refer to the diagram below for a better understanding. Now we have to fill the knapsack in such a way so that the sum of the total weights of the filled items does not exceed the maximum capacity of the knapsack and the sum of the values of the filled items is maximum. We have various items that have different weights and values associated with them. In the 0-1 Knapsack Problem, we are given a Knapsack or a Bag that can hold weight up to a certain value.

We also learn two measures of its efficiency: Time and Space Complexity for all the approaches.

We learn the implementation of the recursive, top-down, and bottom-up approaches to solve the 0-1 Knapsack Problem.

This article defines the 0-1 Knapsack Problem and explains the intuitive logic of this algorithm.

In this article, we will discuss 0-1 Knapsack in detail. There are three types of knapsack problems : 0-1 Knapsack, Fractional Knapsack and Unbounded Knapsack. We have to find the optimal solution considering all the given items. In this problem, we are given a set of items having different weights and values. The Knapsack Problem is an Optimization Problem in which we have to find an optimal answer among all the possible combinations.